谷歌机器学习速成课程:https://developers.google.cn/machine-learning/crash-course/
监督式机器学习 通过学习如何组合输入信息,来对未见过的数据,做出有用的预测
简单的线性回归案例比如 y=w*x+b 标签是要预测的东西,即上面简单案例中的 y 特征是描述数据的输入变量,{x1,x2,x3…xn} 样本数据的特定实例,即 x 有标签样本{特征,标签}:{x,y}用于训练模型 无标签样本{特征,?}:{x,?}用于预测数据
在监督式学习中,训练模型的过程就是不断尝试尽可能减小损失的过程,通过有标签样本来学习(确定)所有权重和偏差的理想值 L1 损失:yi 与实际值 y 的差的绝对值 L2 损失(平方损失) 均方误差 (MSE): 每个样本的平均平方损失
对于 y=w*x+b,首先对 w 和 b 进行初始猜测,然后不断调整直至收敛
对于凸形问题存在一个斜率正好为 0 的位置, 这个最小值就是损失函数收敛之处
梯度:一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大
简而言之,梯度越大意味着导数的绝对值越大,变化率越大 梯度是矢量,具有方向和大小
学习率梯度下降算法的 步长 ,低学习率会花费较长的时间,而学习率过高可能导致永远无法收敛或模型训练结果不准确
超参数是在开始学习过程之前设置值的参数,而不是通过训练得到的参数数据 超参数是编程人员在机器学习算法中用于调整的旋钮 典型超参数:学习率、神经网络的隐含层数量……
实战练习
由于没有现有的样本,所以自己用一个线性方程来产生样本,并加入一些噪声,让样本看起来随机一些,不那么有规律。 方程:y=2*x+1 噪声 0.4
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
#在网页中使用matplotlib显示图像需要设置inline模式
%matplotlib inlinex_data=np.linspace(-1,1,100) # 等差数列生成100个在-1与1之间的点
np.random.seed(5)
y_data=2*x_data+1.0+np.random.randn(*x_data.shape)*0.4
#画出随机生成的样本的散点图
plt.scatter(x_data,y_data)
#画出想要通过学习得到的目标函数
plt.plot (x_data,1.0+2*x_data,'r',linewidth=3)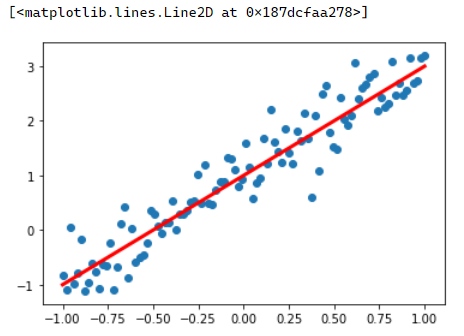
def model(x,w,b):
return tf.multiply(x,w)+b
def loss(x,y,w,b):
err = model(x,w,b)-y # 求差
squared_err = tf.square(err) # 求平方得出方差
return tf.reduce_mean(squared_err) # 求均方差w = tf.Variable(np.random.randn(),tf.float32)
b = tf.Variable(0.0,tf.float32)
training_epochs = 10 # 训练轮数
learning_rate = 0.01 # 学习率#计算梯度函数
def grad(x,y,w,b):
with tf.GradientTape() as tape:
loss_ = loss(x,y,w,b)
return tape.gradient(loss_,[w,b])# 执行训练
step = 0
loss_list = []
display_step = 10
for epoch in range(training_epochs):
for xs,ys in zip(x_data,y_data):
loss_=loss(xs,ys,w,b)
loss_list.append(loss_)
delta_w,delta_b = grad(xs,ys,w,b)
change_w = delta_w*learning_rate
change_b = delta_b*learning_rate
w.assign_sub(change_w)
b.assign_sub(change_b)
step=step+1
if step % display_step == 0:
print("Training Eporch:",'%02d' % (epoch+1),"step:%03d" % (step),
"loss=%.6f" % (loss_))
plt.plot(x_data,w.numpy()*x_data+b.numpy())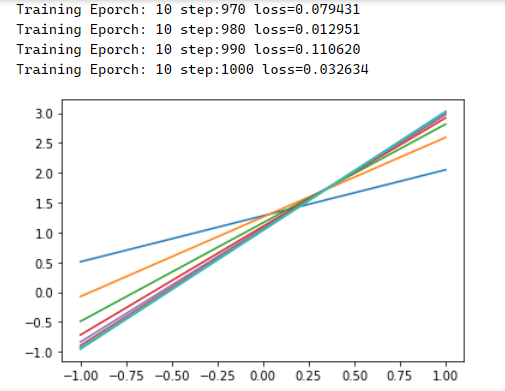
print(“w:“,w.numpy(),“b:“,b.numpy()) 打印:w: 1.9897072 b: 1.0370641,看起来还是比较接近的
#图形化查看损失变化情况 plt.plot(loss_list) plt.plot(loss_list,‘r+‘)
x_test=3.21
predict=model(x_test,w.numpy(),b.numpy())
print("预测值:%f" % predict)
target = 2*x_test + 1.0
print("实际目标值:%f" % target)执行结果
预测值:7.426406
实际目标值:7.420000随机梯度下降法 (SGD)
每次迭代只使用一个样本(批量大小为 1),各个批量的一个样本都是随机选择的
批量梯度下降优化(BGD)
每一次迭代时使用所有样本来进行梯度的更新
总结步骤
生成人工数据集及其可视化 构建线性模型 定义损失函数 (梯度下降)优化过程 训练结果的可视化 利用学习到的模型进行预测